Introduction
The Hubble law for the large scale redshift of galaxies (i.e. redshift proportional to distance) is usually taken as evidence (if not proof) for the picture of an expanding universe in general and the Big Bang theory in particular. However, recessional velocities have by no means been actually measured and the assumption of the Doppler effect being responsible for the shift is only reached due to the absence of other known physical explanations (for the sake of historical correctness it should be pointed out that Hubble himself was apparently never certain about this interpretation of the redshift (see https://web.archive.org/web/20220821071554/http://sites.google.com/site/bigbangcosmythology/home/edwinhubble)). Also, the Hubble law appears to be based on rather limited data sets, and in particular has not been systematically examined for its strict validity throughout the whole of the electromagnetic spectrum, especially for wavelengths of 1m and more where, according to the theory below, one should expect the redshift mechanism to disappear.Plasma Redshift Mechanism
My previous research has already revealed several hitherto unknown effects in the area of ionospheric physics which clearly show the importance of temporal and spatial fluctuations of the random plasma field for the emission and propagation of electromagnetic waves, and I am suggesting that it is the plasma 'micro'field which is also responsible for the redshift of galaxies. The important difference of the intergalactic plasma compared to other plasmas is that, due to its low density, the associated electric field can be considered to be quasi-static and quasi-homogeneous for most electromagnetic waves, not only with regard to the wavelength, but even with regard to the coherence length of the electromagnetic wave field (i.e. the length of the wave trains), as both are much smaller than the distance over which the electric field varies. The latter is directly determined by the average distance of charged particles and could probably be around 1m in intergalactic space. Obviously, this redshift effect would only occur below a maximum wavelength or coherence length and hence there would be a (wavelength dependent) maximum distance beyond which the redshift factor would saturate and approach an asymptotic value. Interestingly, the 3 oK microwave background radiation could in fact be evidence of this: the coherence length of light produced by stars is of the order of 10-2cm (the original coherence length of 100 cm is shortened by collisions in the radiating plasma); with a redshift factor of the order of 104 this would translate into a length of about 100 cm. If the average distance between charged particles in intergalactic space has about the same value, the redshift effect will saturate and hence all stars beyond a certain distance will be redshifted by the same amount (i.e. to 3 oK).Another point to consider in this context is the circumstance that, once the wavetrain is stretched to a length comparable to the distance of charged particles in the plasma, it can not be considered to travel in a homogeneous electric field (gradient) anymore. The stretching of the wavetrain will therefore become randomly inhomogeneous and the coherency of the light will be progressively destroyed, which eventually will lead to its complete indetectability (see my Photoionization Theory for Coherent and Incoherent Light ), hence resolving Olbers' Paradox for a steady state universe.
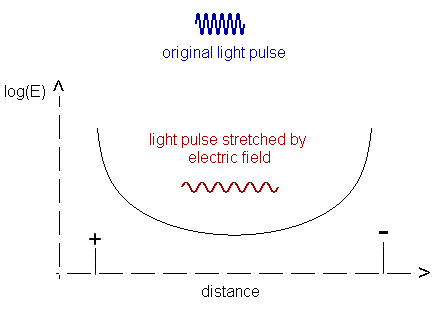Schematic illustration of the suggested redshift mechanismdue to the electric field of free charges in the intergalactic plasma
Quantitative Estimates for Intergalactic Light Propagation
Even though this redshift mechanism has a statistical nature (due to the irregularity of the plasma field), it is very much different from scattering (which has been suggested by other people as being responsible for the redshift (see the Cosmology Discussion page on my website physicsmyths.org.uk for more on this). It could probably be compared to a refraction effect (albeit one independent of wavelength): the point is that here the effect of the plasma field in the direction of propagation of the wave always has the same sign, that is the stretching of the wave (and thus the redshift) is additive (i.e. it is a scalar effect) and will, despite the random nature of the field, result in a very sharply defined redshift.On the other hand, the transverse deviation of the direction of propagation caused by the plasma field has vector properties and thus a random walk character given the isotropy of the medium. So there will be some blurring due to this circumstance, but this should be very small and negligible: if one assumes the intergalactic plasma field to have a scale of about 1m (corresponding to a plasma density of 1m-3) then, over a distance of 1010 lightyears = 1026m, one has 1026 additive redshifts. Now this leads to a redshift of the order of z=1, i.e. in the space of 1m the redshift change is about dz/ds=10-26/m. Assuming that the direction of propagation is changed by the same amount (compared to 360 deg) within 1m, this results over the total distance of 1010 lightyears in a statistical angle of deviation (i.e. a blurring) of Δα=10-26.√1026 .360 deg = 4.10-11 deg, which is negligibly small (for comparison, the angular width of our own galaxy from a distance of 1010 light years would be about 6.10-4 deg , i.e. about 7 orders of magnitude larger; it would take a distance of 7.1014 lightyears until the blurring would become comparable to the apparent size of the galaxy (which would then only be about 10-8 deg; of course, this would be not observable anymore as it is beyond the 'horizon' at about z=104 caused by the spatial scale of the intergalactic plasma field (as mentioned above)). As shown on my page Galactic Redshifts and Supernova Light Curves on my site physicsmyths.org.uk, the suggested mechanism could also explain the apparent delay of supernova lightcurves. For an application of the principles developed on this page to fields of a non-stochastic nature see the page Plasma Theory of 'Gravitational Lensing'.