Introduction
The fact that the solar corona has a temperature of a few million degrees has puzzled solar physicists for a long time, considering the comparatively low temperature of about 6000oK at the sun's apparent surface (the photosphere). Clearly, the laws of thermodynamics seem to rule out that a cool gas volume (the photosphere) should be able to heat another gas volume (the corona) to a temperature of several hundred times its own. Various elaborate plasma processes have been proposed that would enable charged particles in the photosphere to be accelerated to such high temperatures, but all these can still not explain how unordered thermal energy of many particles should be transformed into ordered high energy of a few particles.However, in the course of the 'coronal heating' discussion it has apparently not been recognized that a temperature of several million degrees is in fact the 'natural' temperature of the solar plasma, whereas the photospheric temperature is the 'abnormal' one. In the following, these circumstances are examined in more detail and it will become clear that the 'coronal heating' can be explained in a straightforward way by basic plasma kinetic and atomic processes.
General Energy Considerations
The average gravitational potential energy of an atom of mass m within a spherical mass M with a density distribution ~1/r2 (see below) and radius R is
(1) Epot = -GmM/R (G= gravitational constant). .
(2) Epot= -3.2.10-9erg
According to the Virial Theorem of mechanics, the kinetic energy is related to the potential energy by(3) Ekin= -Epot/2 = 1.6.10-9 erg = 996 eV
Since Ekin=kT (where k is the Boltzmann constant), this corresponds to a temperature(4) T = 1.1.107 oK
which obviously is more than enough to account for the temperature of the solar corona (the average thermal speed of protons for this temperature is about 400 km/sec, which is exactly the average observed speed of the solar wind). The question now is instead: why is the temperature of the photosphere so low compared to the 'gravitational temperature' ? It is clear that classical physics can not be responsible for this, but one has to look for quantum mechanical atomic processes (i.e. inelastic particle collisions) which lead to the photospheric cooling (with the kinetic energy being converted into radiation in the process). This is examined in more detail in the following sections.Density Considerations
Obviously, for inelastic collisions to happen one needs individual neutral atoms, i.e. the average distance between two nuclei in the plasma has to be greater than twice the Bohr radius r0 (r0=5.10-9cm), which means the gas density has to be less than(5) n0=1/[4/3.π.(2r0)3] = 2.4.1023 cm-3
For densities higher than this, no radiative processes are possible at all, i.e. one has a hot but dark plasma 'soup' of protons and electrons (due to their high kinetic energy, the latter are not even able to form larger structures as in fluids or solids). What is now the gas density in the sun ?For a homogeneous sphere, it would simply be given by
(6) nh=M/(4/3.π.R3.m)
where M is the total solar mass, R the solar radius and m the weight of a hydrogen atom.This yields
(7) nh = 8.7.1023 cm-3 .
However, the assumption of a homogeneous gas sphere is not adequate here, because a gas sphere in hydrostatic equilibrium necessarily has a density decreasing with the distance r from its center ~ 1/r2 (assuming isothermal conditions; see the Star Formation page).The density n(R) near the surface of the sun (located at a radius R) has therefore to be determined by the equation
(8) M = n(R).m.4π. 0∫Rdr' r'2.(R/r')2 = n(R).m.4π.R3 , i.e.
(9) n(R) = M/(4.π.R3.m) = 2.9.1023 cm-3
As this is virtually identical to the maximum density for inelastic collisions (Eq.(5)), the latter can consequently only occur in a very narrow layer near the surface of the sun (causally, it is of course this density which determines where the apparent surface (the photosphere) is located). As the density increases towards the centre of the sun, no inelastic collisions can occur below the photosphere and consequently the plasma will not be cooled but have the 'gravitational temperature' of 1.1.107 oK. The situation is illustrated schematically below below: Fig.1 shows the cross section through a gas sphere in classical hydrostatic equilibrium, Fig.2 the additional effect of quantum mechanical inelastic collisions.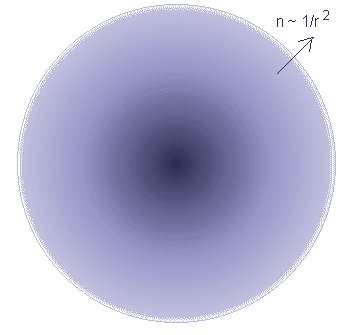
Fig.1: Gas ball in hydrostatic equilibrium according to classical physics
(density decreases only slowly outwards)
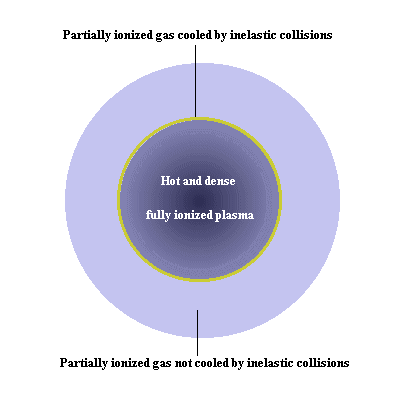
Fig.2: Gas ball in hydrostatic equilibrium + cooling by inelastic collisions
(strong density decrease in collision region)
Details of the Inelastic Collision Process
The formation of striations in glow discharges as well as artificial ionospheric airglow experiments (see the Airglow Excitation paper) demonstrate the existence of a resonant collisional excitation process with a cross section identical to the resonant scattering of radiation. Although in the context of these phenomena one deals with inelastic collisions of electrons, one can assume that the same process applies to protons (or ions in general) as well, with the required energies scaled upwards by a factor mp/me (with mp the proton mass and me the electron mass).The crucial point here is that the high plasma density in the photosphere broadens the atomic states energetically by such an amount the usual radiative transition lines blend into a continuum (see the Research Home Page (under 'Emission and Propagation ...')), i.e. excitation is possible for all energies as long as the latter is less than the ionization energy (=13.6 eV). The latter condition means that most of the electrons of the 1.1.107 oK (=996 eV) plasma will be unable to excite any radiative transitions, but for protons the mass scaling factor (=1/1836) means that keV energies appear now merely in the eV range, i.e. they can excite the atomic transitions. As a result of the inelastic collision, the proton will lose practically all of its kinetic energy, but will subsequently be somewhat heated again by elastic collisions with the high energy electrons. According to classical mechanics, elastic collisions should indeed equalize the temperatures between the electrons and protons after a number of collisions, but the loss of (radial) kinetic energy of an electron in the course of a close Coulomb collision means that the electron has a high probability to recombine with the proton, i.e. it loses all its kinetic energy on recombination apart from the fraction that has been transferred in this one collision. Classical mechanics shows that the relative collisional energy transfer between two very different masses is given by the mass ratio, i.e. in this case a fraction 1/1836 of the electron temperature of 1.1.107 oK , which results in the photospheric temperature
(10) Tph ≈ 6000 oK
in agreement with the observed value.(it is worth noting that it is indeed the recombination of the electrons and protons that produces the radiative output of the photosphere and not the cooling of the protons due to the inelastic collisions with neutral atoms (the contribution of the latter is orders of magnitudes smaller)). In order for the density to decrease from a value of around 1023 cm-3 at the sun's surface to about 108 - 105 cm-3 in the solar corona, the inelastic collision process has to reduce the flux of protons by a factor 10-15-10-18. According to the exponential absorption law, this requires about 35-40 mean free paths
(11) lex = 1/(Nn.σex).
where Nn is the neutral atom density and σex the inelastic collision cross section.lex should therefore have a value of around 1/40 of the scale height of the photosphere, which results in
(12) lex = 5 km .
A neutral density of 108 cm-3 and an excitation cross section of 10-14 cm2 would about yield this length, and both of these values can be shown to be reasonable estimates for the photosphere (an exact determination would require a more elaborate consistent treatment however). Although the neutral atom density hardly decreases higher up in the solar atmosphere (due to the low plasma densities recombination is not quenched by elastic collisions and the degree of ionization is roughly 50%), the low plasma density also means that the spectral lines are not collisionally broadened to a continuum any more. Inelastic collisions for the protons can therefore only occur in very narrow energy bands coinciding with the usual spectral lines and most protons will not suffer any energy loss in this respect, i.e. there is only a relatively small amount of cooling above the photosphere for those protons that penetrate the latter without suffering any inelastic collisions (which explains why the coronal temperature is actually only a few times 106 oK rather than 1.1.107 oK; the solar wind on the other hand consists of particles that do not suffer any inelastic collisions above the photosphere either and thus have the original gravitational energy).