Coulomb Collision Cross Section and Coulomb Logarithm

In all corresponding treatments in the literature, the total cross section for Coulomb scattering, as derived over the differential cross section, is obtained as a divergent expression unless an arbitrary cut-off value for the impact parameter (or scattering angle) is introduced (this leads to the well known Coulomb Logarithm factor). The following analysis shows that a finite effective total cross is in fact obtained if the exact scattering geometry is properly taken into account with regard to the energy transfer function.

As usual, the starting point of the derivation is the well known Rutherford-formula for the differential cross section

(1)       dσ_c(ε,Θ')/dΩ' = Z^2.e⁴ / [16^.ε^2.sin⁴(Θ'/2) ] ,

where Z is the nuclear charge number, e the elementary charge, ε the center of mass energy of the two charges and Θ' the scattering angle in the center of mass system (note that this expression is for cgs-units; in SI-units it requires a further numerical factor 8.08^.10¹⁹ (the square of the 'Coulomb constant')).

The second aspect entering into the problem is the dependence of the energy transfer function on the scattering angle. This can be determined by considering the energy transferred to a surface element dS of a spherical target in an elastic collision with a homogeneous particle beam. The surface element may be hereby defined by the angles η and η+dη (Fig.1).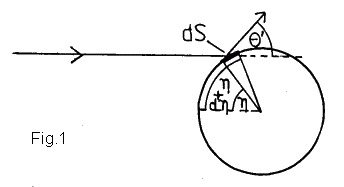

η=0..π/2 designates in general the angle between the velocity vector of the incident particle before the collision and the velocity vector of the target particle (initially assumed at rest) after the collision. The scattering angle Θ' is hereby related to η by the general expression for elastic collisions

(2)       η = (π-Θ')/2 .

The amount of energy transferred to the surface element dS is determined by two factors : a) the amount of energy transferred by a single particle hitting the surface element dS and b) the number of particles (or probability of the single particle) hitting dS.
The first factor (a) is well known to be given by the formula (see for instance Landau and Lifschitz, Mechanics)

(3)       Δ(Θ') = 4^.m₁^.m₂^.sin²(Θ'/2) / (m₁+m₂)² ,

where Δ(Θ') designates the relative energy change as a function of the scattering angle Θ' (related to the surface element by Eq.(2)). m₁ and m₂ are the particle masses, where m₂ is assumed at rest in the laboratory system before the collision (at this stage of the derivation m₁ and m₂ are arbitrary; when evaluating the total cross section, the use of the center of mass variable Θ' implies m₁<<m₂ which does however not restrict the general validity of the so obtained qualitative results).
The second factor (b) is obviously proportional to cosη (for the case of a homogeneous particle beam, i.e. a homogeneous probability distribution of impact parameters). One can thus define a corresponding distribution function

(4)       f(η) = 1/π^.cos(η) ,

where f(η) is normalized to half the sphere surface which is exposed to the incident particle beam, i.e.

(5)       _(2π)∫dΩ_H f(η) = 1 .

(This normalization is of importance only for the definition of the average energy transfer Δ_av . For the evaluation of the total cross section a different normalization is necessary (see Eq.(8))).
By means of Eq.(2), one obtains f as a function of the scattering angle (center of mass) i.e.

(6)       f(Θ') = 1/π^.sin(Θ'/2) .

Eq.(6) maps a homogeneous distribution of impact parameters into Θ'-space, i.e. it provides the geometrical connection between the monodirectional incident particle beam and the spherical scattering surface. This connection is ignored in the literature throughout, which invalidates in these cases the interpretation of the scattering angle Θ' as an independent integration variable in Eqs.(11) and (12) (see below). The identification of the scattering angle Θ' with the polar angle of a coordinate system fixed in the target center is only correct if the exact geometrical relations in the scattering process on a microscopical scale are of no importance. This is however not the case when considering the energy transfer function, and the neglection of this aspect is the reason for the well known logarithmic divergence of the total cross section for Coulomb scattering (Coulomb Logarithm) in other treatments of this problem.

The total amount of energy transferred to the surface element is thus given by the product of Eqs.(3) and (6), i.e. the corresponding normalized energy transfer function is of the form

(7)       F(Θ') = c_F^.sin³(Θ'/2) ,

where c_F is a normalization constant which is obtained from the condition

(8)       _(4π)∫dΩ F(Θ') = 1

as

(9)       c_F = 5/(8π) ,

i.e.

(10)       F(Θ') = 5/(8π) ^.sin³(Θ'/2) ,

Eq.(10) describes the distribution of the energy transfer over scattering angle. The normalization (Eq.(8)) is such that it corresponds to the average fractional energy loss

(11)       Δ_av = 1/4π^._(4π)∫dΩ' Δ(Θ')^.f(Θ') = 8/(5π) ^.m₁^.m₂/(m₁+m₂)² =
                       = 8/(5π) ^.m₁/m₂       if m₁<<m₂ (see remarks below Eq.(12)).

The total cross section for Coulomb scattering (with regard to the average energy transfer) is now given by

(12)       σ_c(ε) = _(4π)∫dΩ' F(Θ') ^.dσ_c(ε,Θ')/dΩ'

Since the integrations in Eqs.(11) and (12) are performed in the center of mass system, whereas the cross section shall constitute a quantity in the laboratory system, it is clear that these definitions are strictly (i.e. quantitatively) valid only for m₁<<m₂, in which case the scattering angles in those two frames of reference nearly coincide.
With this restriction, one gets from Eqs.(1),(10) and (12)

(13)       σ_c(ε) = 5/16 ^.Z^2.e⁴ / ε² .

(this expression is for cgs-units; in SI-units it requires a further numerical factor 8.08^.10¹⁹ (the square of the 'Coulomb constant')).
One should note again that ε is the centre of mass energy of both particles, which for m₁>>m₂ differs from the energy of the incident mass m₁ in the rest frame of m₂ by a factor (m₁+m₂)/m₂, i.e. if ε is taken as the energy of m₁, this results then in a further factor ((m₁+m₂)/m₂)² for the cross section. On the other hand, the energy transferred in a single collision is only a factor 8/(5π)^.m₁^.m₂/(m₁+m₂)² (see Eq.(11)), so as far as the effective cross section for a total energy loss of the incident particle is concerned, Eq.(13) has to be multiplied by  8/(5π) ^.m₁/m₂  in case of the incident projectile mass m₁>>m₂ (with ε then understood as the energy of m₁ in the rest frame of m₂) (this explains for instance the much shorter mean free path of high energy ions in matter compared to electrons of the same energy, namely because their collision cross section with the atomic electrons is much larger).

In any case, with Eq.(13) a finite expression for the total cross section has been obtained, contrary to the usual but erroneous treatment of the problem where neglection of the additional factor Eq.(6) leads to the well known logarithmic divergence (Coulomb Logarithm) of the total cross section. Taking the correct energy transfer function (Eq.(10)) into account, the sin^-4(Θ'/2) behaviour of the Rutherford formula is exactly cancelled by F(Θ') since additionally there adds a further factor sin (Θ'/2) ) from the differential dΩ' in Eq.(12). Obviously, the 1/r - potential is the most slowly decreasing potential function for which a finite total cross section can be obtained , because for geometrical reasons no potentials decreasing asymptotically slower than 1/r are thinkable. The notion of 'infinite-range' potentials must therefore be abandoned , since the effective total cross section (as a physical quantity) always has a finite value independent of macroscopic parameters of the associated plasma.

Print Version

Home

Search Site